盛最多水的容器

概要：给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量

示例：

输入：nums = [1,8,6,2,5,4,8,3,7]
输出：49
解锁：由长度为8的左边界和长度为7的右边界构成的容器容量最大，(8-1)*Math.min(nums[8], nums[1])=49

输入：height = [1,1]
输出：1

提示：

n == height.length
2 <= n <= 105
0 <= height[i] <= 104

心路历程

看到这个题目，我第一时间想到的就是定义一个maxArea记录最大容量，然后遍历，再用一个指针固定指向left边界，另一个指针指向right边界并依次向后移动，找出left指针可以得到的最多容量，最终遍历完数组后得到的maxArea即为最终答案。

/**
 * @param {number[]} height
 * @return {number}
 */
var maxArea = function (height) {
  // 我的想法是遍历，用一个指针固定指向left边界，另一个指针指向right边界并依次向后移动，找出left指针可以得到的最多容量
  let maxArea = 0;
  for (let i = 0; i < height.length; i++) {
    for (let j = i + 1; j < height.length; j++) {
      // 求最大容量
      maxArea = Math.max(maxArea, Math.min(height[i], height[j]) * (j - i));
    }
  }
  return maxArea;
};

写好代码后，我兴高采烈的拿去运行，您猜怎么着，嘿，超时了。如果数组很大的话，双重遍历确实耗时太多了。好吧，这道题，我做不出来，投降看题解，学习下别人的思路。

首先别人是先假设出x,y两边，并得到最大值的计算公式，通过公式来推出影响最大值的因素以及变化规律，最后再写代码。这种解题思路值得学习。

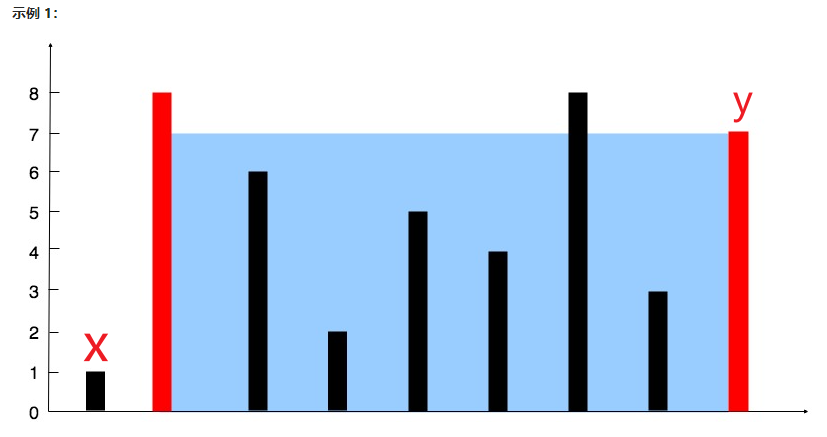
来看看这个二次元的桶，容量由两个因素决定，长*宽。假设，左边界的元素编号为x，右边界的元素编号为y，那么得到的容量公式就为：

1	s(x,y) = Math.min(height[x], height[y]) * (y - x)

也就是短边*长，现在我们来思考下，为什么我上面是用的双重for循环，是因为我没有一开始就固定其中一个变量，导致只能在循环中固定。如果x，y分别在数组的两端，那么此时长为最大值，此时影响容量的因素就只剩下短边了，那如果分别移动两条边会发生什么：

如果将指向短边的指针向中心移动一位，此时长度会-1，下一个边可能会比之前的短边更长或更短，s的值可能会增大或者减小
如果将指向长边的指针向中心移动一位，此时长度会-1，下一个边无论比之前的长边更长或更短，s的值一定会减小，因为宽是取的短边的值

如果两条边都一样长，无论移动哪一边，此时长度会-1，s的值一定会减小，所以无论移动哪一边都一样，最终得到的最大值都是对的，如果想不明白可以画图试试，如果中间有两个更长的边，那早晚为将指针移动到这个两个边上去，如果中间只有一个更长的或者没有更长的，那最大值还不是开始的那个值。也就是每轮向内移动短板，所有消去的状态都 不会导致面积最大值丢失，那让我们来看看代码吧

var maxArea2 = function (height) {
  if (height.length < 2) return 0;
  let maxArea = 0;
  let right = height.length - 1;
  let left = 0;
  while (left < right) {
    // 计算出最大容量
    maxArea = Math.max(
      maxArea,
      (right - left) * Math.min(height[left], height[right])
    );
    // 向中间移动短边所在的指针
    if(height[left] < height[right]){
      left++;
    }else{
      // 两边相等的话，移动哪条边都无所谓
      right--;
    }
  }
  return maxArea;
};

简单来说就是从两端开始，向内收缩最短边。

最终代码

var maxArea = function (height) {
  if (height.length < 2) return 0;
  let maxArea = 0;
  let right = height.length - 1;
  let left = 0;
  while (left < right) {
    // 计算出最大容量
    maxArea = Math.max(
      maxArea,
      (right - left) * Math.min(height[left], height[right])
    );
    // 向中间移动短边所在的指针
    if(height[left] < height[right]){
      left++;
    }else{
      // 两边相等的话，移动哪条边都无所谓
      right--;
    }
  }
  return maxArea;
};